Comments towards a theoretical foundation of clustering
Posted with : Clustering, Data science
This post is based on the notes I took last month in the PCMI’s Mathematics of Data program during conversations with Shai Ben-David and Bianca Dumitrascu about Shai’s research on the theoretical foundations of clustering.
Clustering
Given some data, the clustering problem consists of partitioning the data in subsets with an specific criterion.
This is a very fundamental problem in machine learning. It is usually a necessary step for solving many data related problems (see for example the digit classification problem of my previous post).
Model selection
- Q: What is a good clustering?
- A: You “know it when you see it”.
Can you guess the good clusters in the following image (from scikit-learn)?
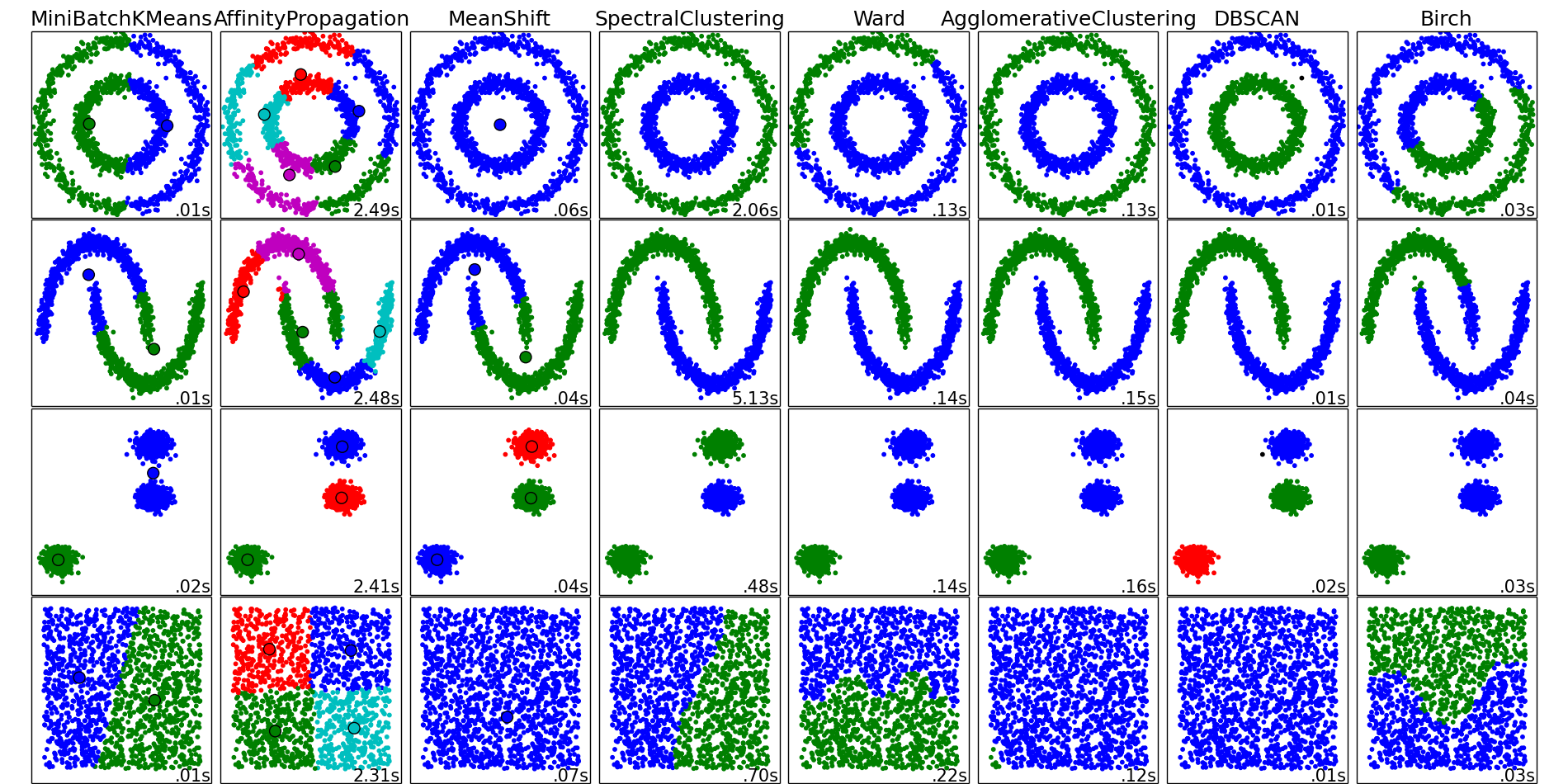
Real data doesn’t look like the toy datasets, specially when the data is high dimensional. And the clustering criterion one should use depends on the application. Each clustering task has a different objective and, of course, there is no universally best algorithm. Good cluster features may be
- Balance clusters sizes
- Robustness to outliers
- Separate dissimilar points
- Join similar points
Different problems require different features. For example, when designing school districts one may want to balance cluster sizes, and when merging different medical records (hopefully from the same patient) one should focus on separating dissimilar points.
Clustering strategies
There are many different clustering algorithms and clustering objectives. I’ll focus on two of them.
Linkage-based clustering
This strategy consists on starting with every point being its own cluster and iteratively merging the closest two clusters (according to some proximity measure) until every point belongs to the same cluster. If the target number of clusters is , the process is stopped when clusters are reached. This process is represented by a tree structure like this one from Wikipedia:
Kmeans clustering
Divide the data set in sets that minimize the sum of the (squared) distance from each point to the (geometric) center of the cluster.
This problem is thought to be very hard to solve (NP-hard) so it cannot be ‘solved’ in general, but different algorithms are known to work in different settings (like the one I showed in my previous post). I’ll come back to the hardness of kmeans later on this post.
Characterization of linkage-based algorithms
Shai Ben-David and collaborators have worked on characterizing clustering according to the output clusters. In particular for linkage-based algorithms.
I don’t want to get too technical here so I’ll just mention some properties satisfied by single linkage algorithm and refer to the paper for the complete characterization:
- The output only depends on the order of the distances (and not the distances themselves). This property makes the algorithm good against outliers, since too large distances won’t change the outcome. This property may also allow the user incomplete partial comparison for clustering purposes (this is slightly related with this post).
- Locality: let’s say we run the algorithm and it gives as clusters. If you take clusters away and you run the algorithm for clusters, you get the same result as before, meaning that the clusters together with the clusters coincide with the original clusters.
- Increasing (the number of clusters) results in only breaking up an already existing cluster.
Understanding what your algorithm does will tell you what it is good for. I think that is the purpose (and moral) of the characterization of algorithms.
Clustering is not actually hard
I mentioned that kmeans is NP-hard. But that ‘hardness’ is a worst case complexity, which may be irrelevant in reality, if most problems are actually easy. One good example of that is compressed sensing.
Another point of view is that, maybe if the data is hard to cluster, then we shouldn’t be trying to cluster it. There is a line of research which defines different notions of clusterability for data. For example:
- Robustness to perturbation:
- Adding random noise to the data does not change the clusters (for some noise threshold)
- Multiplying the distances by a small factor does not changes the clusters.
- Center proximity stability
- Every point is closer to its cluster center than to every other center by some factor.
The research in this field provides specific quantifications to the previous (and other) clusterability notions. It also provides proofs of the form “if data satisfies condition X then it’s easy to cluster it with algorithm Y in time at most f(X)”. However there is no efficient way to test clusterability in a given data set. And we are not close to having a satisfactory (and practical) theoretical foundation of clustering.